Małżeńskie korelacje
Diagnoza Społeczna to cykl badań, który zakończono niemal dziesięć lat temu, jednak publicznie udostępnione dane z przeprowadzonych w ramach Diagnozy ankiet wciąż pozwalają odkrywać ciekawe zależności i wzorce.
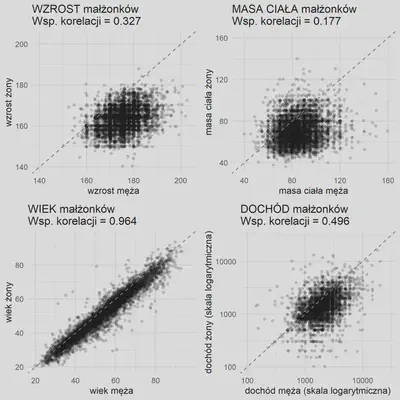
Przykładem takich zależności, które można przedstawić na przykładzie zbiorów danych zgromadzonych w ramach diagnozy są korelacje pomiędzy małżonkami. Sprawdźmy, jak wygląda korelacja miedzy żoną i mężem, jeżeli chodzi o wiek, wzrost, masę ciała i dochód.
Dane z ankiet można odnaleźć na githubie, prof. Przemysław Biecek przygotował pliki, które można od razu wciągnąć do R. Poniższe polecenie wciąga ramkę danych o nazwie osoby:
load(url("https://github.com/pbiecek/Diagnoza/raw/master/data/osoby.rda"))
Z danych wybieramy tylko te zmienne, które są nam potrzebne: identyfikatory, płeć, wiek, wzrost, masa ciała, dochód oraz wagi ankietowe. Z opisu danych przygotowanego przez prof. Biecka wiem, że zmienne dotyczące roku 2015 mają nazwy zaczynające się od litery h.
extract <- osoby[, c('numer_gd', 'numer_osoby', 'hc5', 'hc6', 'hc10',
'hp65', 'hp52', 'hp53', 'waga_2015_ind', 'wiek2015')]
names(extract) <- c('household_id', 'person_id', 'family_no', 'family_role',
'sex', 'income', 'height', 'weight', 'survey_weight', 'age')
Ponieważ źródłowa ramka danych obejmuje wszystkie lata badania, wiele rekordów zawiera wartości brakujące (NA). Po serii prób i inspekcji danych uznałem, że najskuteczniejsze będzie następujące podejście: tymczasowo zastąpić NA wartością -1 w kolumnie dochodu (ponieważ nie chcemy usuwać obserwacji z brakującym dochodem, np. emerytów), następnie usunąć wiersze zawierające inne braki danych, a na końcu ponownie przywrócić NA w zmiennej dochód.
extract$income[is.na(extract$income)] <- -1
extract <- na.omit(extract)
extract$income[extract$income == -1] <- NA
Następnie tworzymy identyfikator rodziny (family_id), aby połączyć dane o mężu i żonie.
extract$family_id <- paste(extract$household_id, extract$family_no)
Z danych wybieramy osobno mężów i żony.
extract_husband <- extract[(extract$family_role == 1 | extract$family_role == 2) & extract$sex == 1,
c('family_id', 'income', 'height', 'weight', 'survey_weight', 'age')]
names(extract_husband) <- c('family_id', 'husband_income', 'husband_height', 'husband_weight',
'husband_survey_weight', 'husband_age')
extract_wife <- extract[(extract$family_role == 1 | extract$family_role == 2) & extract$sex == 2,
c('family_id', 'income', 'height', 'weight', 'survey_weight', 'age')]
names(extract_wife) <- c('family_id', 'wife_income', 'wife_height', 'wife_weight',
'wife_survey_weight', 'wife_age')
Po połączeniu danych o małżonkach otrzymujemy ramkę e, w której każdy wiersz odpowiada jednej parze.
e <- merge(extract_husband, extract_wife)
Autorzy badania dostarczyli wagi ankietowe, dzięki którym można skorygować otrzymane wyniki, żeby uwzględnić fakt, że nie każda osoba miała jednakowe szanse na znalezienie się w próbie. Przyjmuję, że waga ankietowa dla pary to średnia z wag ankietowych męża i żony. Przekształcam wagi tak, żeby ich suma była równa liczbie małżeństw w próbie.
e$avg_survey_weight <- (e$husband_survey_weight + e$wife_survey_weight)/2
e$avg_survey_weight <- e$avg_survey_weight / mean(e$avg_survey_weight)
head(e)
## family_id husband_income husband_height husband_weight husband_survey_weight
## 1 100004 1 4000 176 79 0.5515697
## 2 100009 1 2400 182 90 0.5929627
## 3 100014 2 2800 181 120 1.4742120
## 4 100015 1 1800 170 87 0.9607670
## 5 100018 1 3000 175 82 0.7655140
## 6 100021 1 1400 185 92 0.3082680
## husband_age wife_income wife_height wife_weight wife_survey_weight wife_age
## 1 66 1000 157 51 0.4846472 58
## 2 42 1400 168 57 0.6888809 39
## 3 43 1000 172 80 1.4206220 45
## 4 64 1300 160 68 0.8562090 62
## 5 47 2000 159 75 0.7330340 45
## 6 47 1000 170 104 0.2951890 47
## avg_survey_weight
## 1 0.5390513
## 2 0.6668290
## 3 1.5059241
## 4 0.9452107
## 5 0.7795610
## 6 0.3139249
Zbadajmy cztery wymiary podobieństwa par:
-
wzrost,
-
masa ciała,
-
wiek,
-
dochód.
Dla każdego obliczymy współczynnik korelacji Pearsona z uwzględnieniem wag ankietowych.
cor_height <- cov.wt(data.frame(e$husband_height, e$wife_height),
wt = e$avg_survey_weight, cor = TRUE)$cor[2,1]
library(ggplot2)
min_val <- min(e$husband_height, e$wife_height, na.rm = TRUE)
max_val <- max(e$husband_height, e$wife_height, na.rm = TRUE)
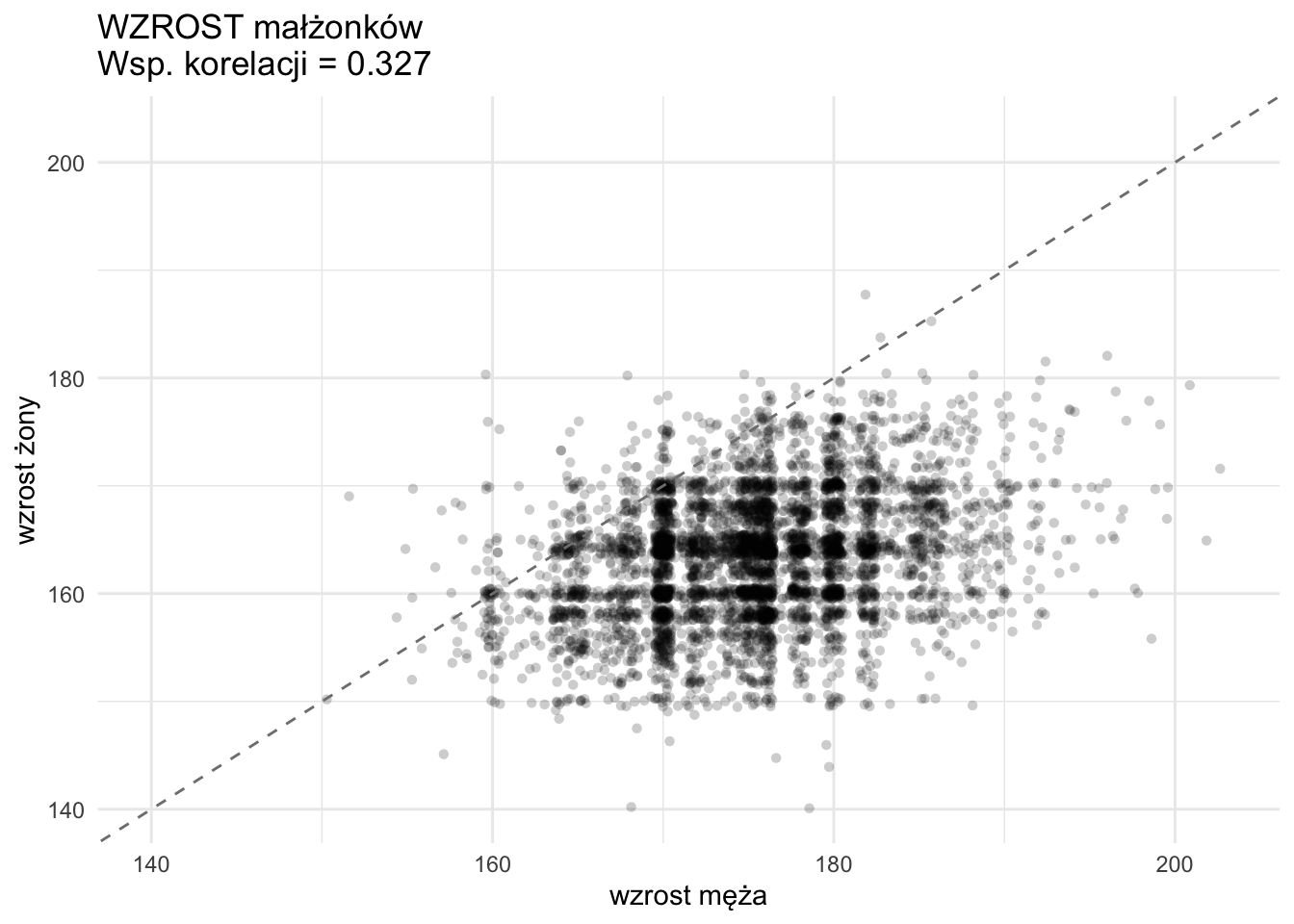
G1 <- ggplot(e, aes(x = husband_height, y = wife_height)) +
geom_jitter(alpha = 0.2, width = .5, height = .5, shape = 16) +
geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "grey50") +
scale_x_continuous(limits = c(min_val, max_val)) +
scale_y_continuous(limits = c(min_val, max_val)) +
labs(
x = "wzrost męża",
y = "wzrost żony",
title = paste0("WZROST małżonków \n", "Wsp. korelacji = ", round(cor_height, 3))
) +
theme_minimal()
G1
cor_weight <- cov.wt(data.frame(e$husband_weight, e$wife_weight),
wt = e$avg_survey_weight, cor = TRUE)$cor[2,1]
library(ggplot2)
min_val <- min(e$husband_weight, e$wife_weight, na.rm = TRUE)
max_val <- max(e$husband_weight, e$wife_weight, na.rm = TRUE)
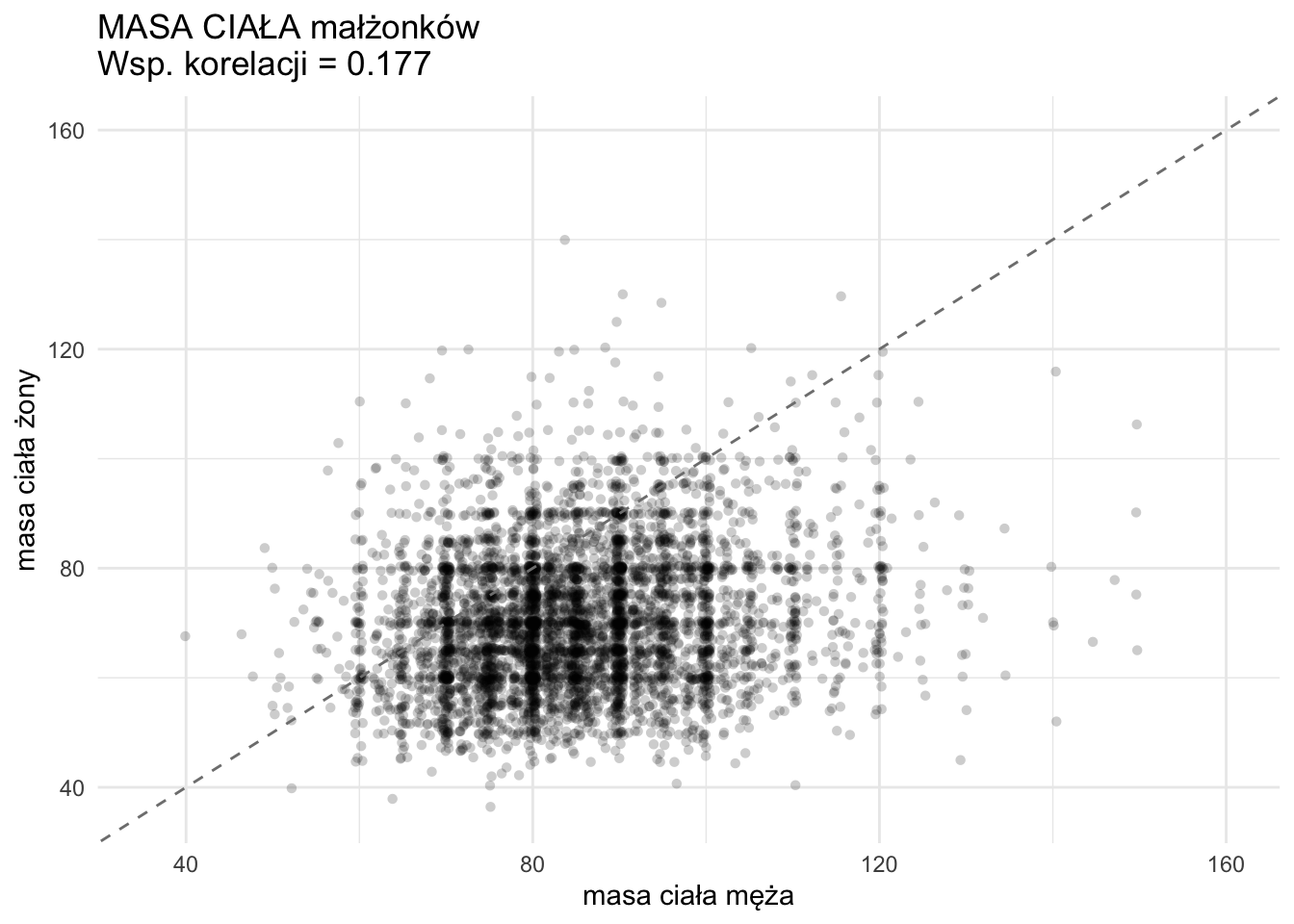
G2 <- ggplot(e, aes(x = husband_weight, y = wife_weight)) +
geom_jitter(alpha = 0.2, width = .5, height = .5, shape = 16) +
geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "grey50") +
scale_x_continuous(limits = c(min_val, max_val)) +
scale_y_continuous(limits = c(min_val, max_val)) +
labs(
x = "masa ciała męża",
y = "masa ciała żony",
title = paste0("MASA CIAŁA małżonków \n", "Wsp. korelacji = ", round(cor_weight, 3))
) +
theme_minimal()
G2
cor_age <- cov.wt(data.frame(e$husband_age, e$wife_age),
wt = e$avg_survey_weight, cor = TRUE)$cor[2,1]
library(ggplot2)
min_val <- min(e$husband_age, e$wife_age, na.rm = TRUE)
max_val <- max(e$husband_age, e$wife_age, na.rm = TRUE)
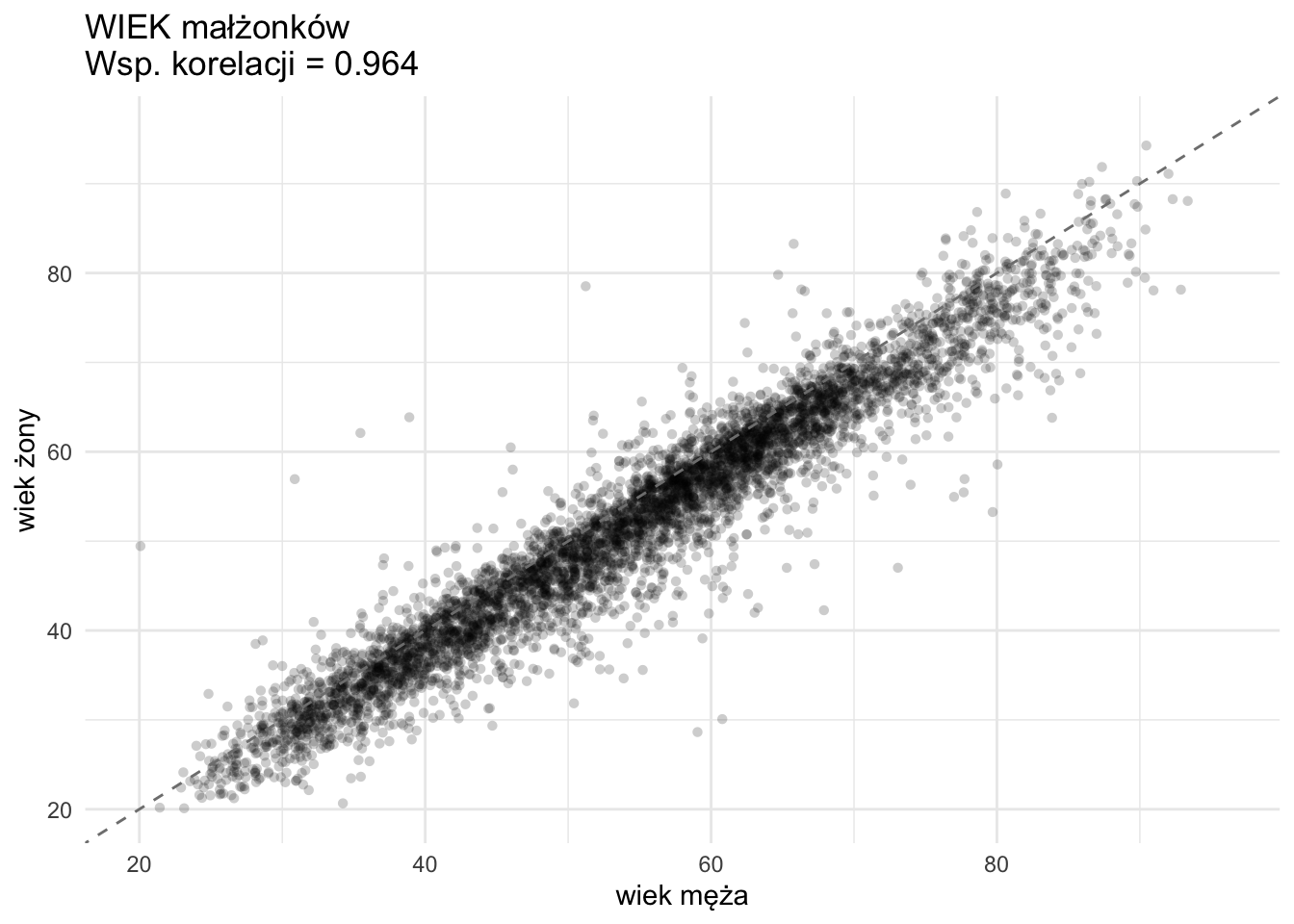
G3 <- ggplot(e, aes(x = husband_age, y = wife_age)) +
geom_jitter(alpha = 0.2, width = .5, height = .5, shape = 16) +
geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "grey50") +
scale_x_continuous(limits = c(min_val, max_val)) +
scale_y_continuous(limits = c(min_val, max_val)) +
labs(
x = "wiek męża",
y = "wiek żony",
title = paste0("WIEK małżonków \n", "Wsp. korelacji = ", round(cor_age, 3))
) +
theme_minimal()
G3
e2 <- na.omit(e[, c('husband_income', 'wife_income', 'avg_survey_weight')])
cor_income <- cov.wt(data.frame(e2$husband_income, e2$wife_income),
wt = e2$avg_survey_weight, cor = TRUE)$cor[2,1]
library(ggplot2)
min_val <- min(e2$husband_income, e2$wife_income, na.rm = TRUE)
max_val <- max(e2$husband_income, e2$wife_income, na.rm = TRUE)
G4 <- ggplot(e2, aes(x = husband_income, y = wife_income)) +
geom_jitter(alpha = 0.2, width = .01, height = .01, shape = 16) +
geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "grey50") +
scale_x_log10(limits = c(min_val, max_val)) +
scale_y_log10(limits = c(min_val, max_val)) +
labs(
x = "dochód męża (skala logarytmiczna)",
y = "dochód żony (skala logarytmiczna)",
title = paste0("DOCHÓD małżonków \n", "Wsp. korelacji = ", round(cor_income, 3))
) +
theme_minimal()
G4
