Jak zważyć psa linijką w R
Jutro w ramach Bałtyckiego Festiwalu Nauki po raz kolejny poprowadzimy ze studentami Analityki Gospodarczej na Wydziale Zarządzania i Ekonomii PG zajęcia ze statystyki dla uczniów szkół podstawowych zatytułowane “Jak zważyć psa linijką”. Za materiały dziękujemy Brygadzie Miar.
Pierwszym zadaniem, z którym zmierzą się uczestnicy warsztatów, jest oszacowanie masy psa na podstawie jego wielkości. Poniżej fragment komiksu przygotowanego kilka lat temu przez prof. Przemysława Biecka.
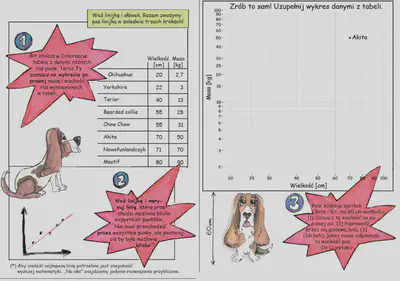
Uczniowie będą to zadanie wykonywać “na oko”, jednak studenci po zajęciach ze statystyki mogą przeprowadzić obliczenia zgodnie z regułami sztuki. Oto wykres, który na podstawie prostej regresji dopasowanej metodą najmniejszych kwadratów przewiduje masę psa, którego spotkali Beta i Bit:
Poniżej przedstawiam propozycję rozwiązania zadania w R.
Stwórzmy najpierw tabelę (data frame, ramkę danych):
size<-c(20, 22, 40, 55, 55, 70, 71, 80)
mass<-c(2.7, 3, 13, 28, 31, 50, 70, 90)
labels<-c("Chihuahua", "Yorkshire", "Terier", "Bearded collie",
"Chow Chow", "Akita", "Nowofundland", "Mastif")
df<-data.frame(size, mass, labels)
df
## size mass labels
## 1 20 2.7 Chihuahua
## 2 22 3.0 Yorkshire
## 3 40 13.0 Terier
## 4 55 28.0 Bearded collie
## 5 55 31.0 Chow Chow
## 6 70 50.0 Akita
## 7 71 70.0 Nowofundland
## 8 80 90.0 Mastif
Przedstawmy dane na wykresie:
library(ggplot2)
library(ggrepel)
ggplot(data=df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
theme_bw() +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels))
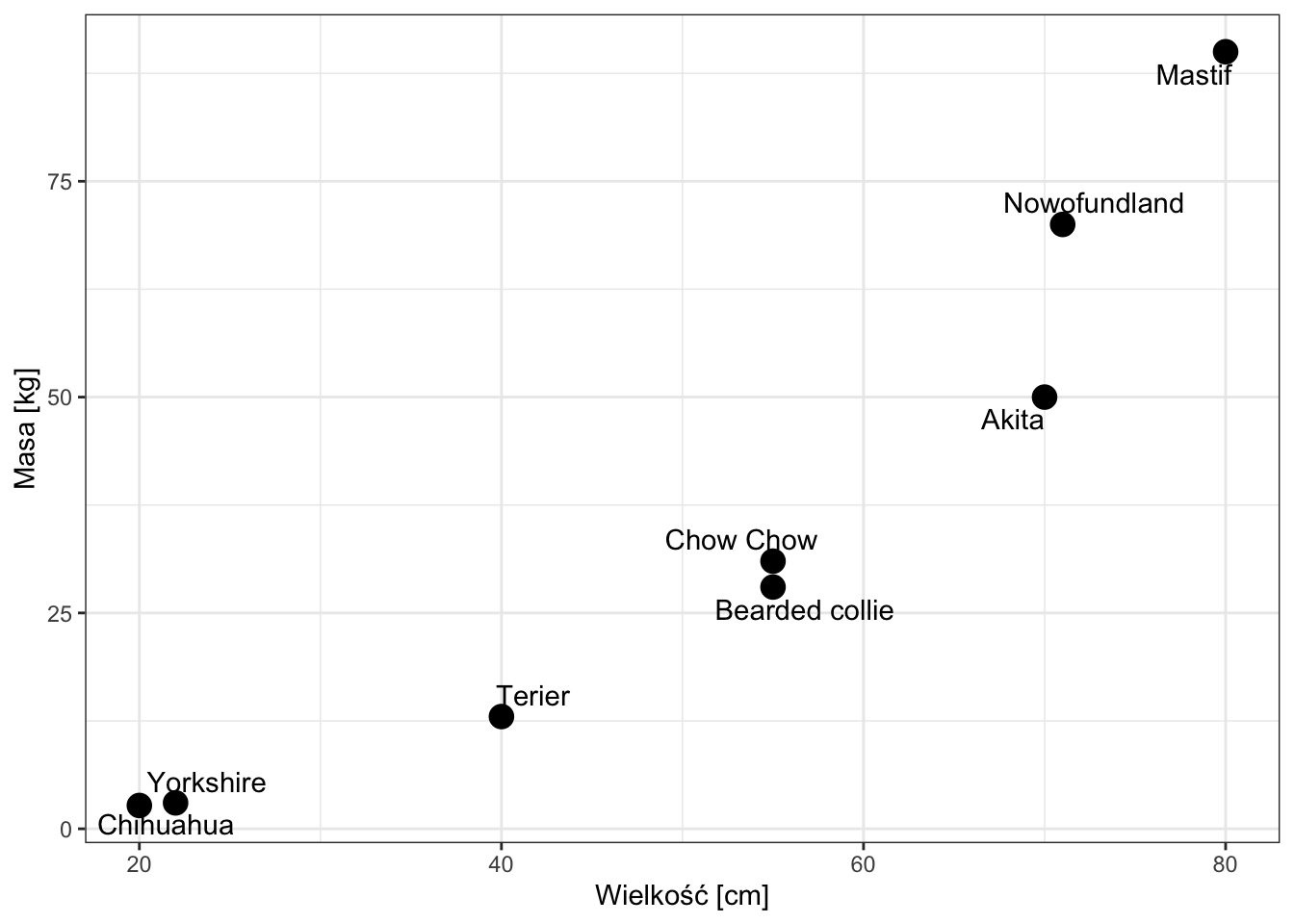
Wygląda na to, że zależność pomiędzy wielkością a masą nie jest liniowa. Będziemy więc stosować model potęgowy. W takiej sytuacji, aby użyć regresji liniowej, zarówno zmienna X (objaśniająca, czyli wielkość) i zmienna Y (przewidywana, czyli masa) powinny zostać zlogarytmowane.
Nie powiemy tego dzieciom, ale w ich komiksie zarówno wielkość, jak i masa są przedstawione za pomocą skali logarytmicznej (proszę jeszcze raz spojrzeć na zamieszczony powyżej fragment komiksu). Spróbujmy to odtworzyć w R:
yticks<-c(2,3,4,5,6,7,8,9,10,15,20,25,(3:10)*10)
xticks<-c(20, 25, (3:10)*10)
ggplot(df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
scale_y_continuous(trans='log10', breaks=yticks) +
scale_x_continuous(trans='log10', breaks=xticks) +
theme_bw() +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels))
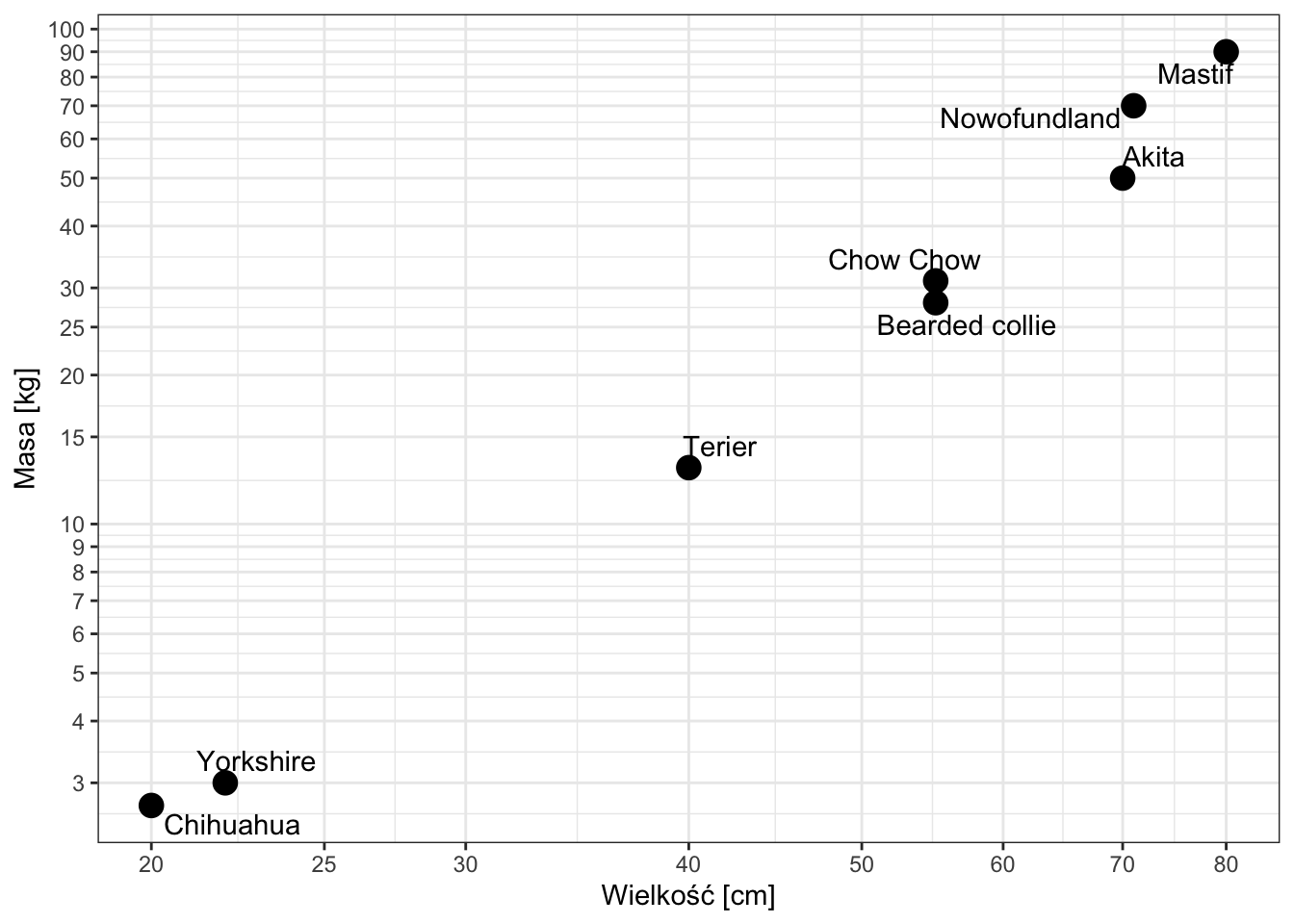
Jak widać, teraz poprowadzenie prostej linii w przybliżeniu dopasowanej do punktów jest możliwe.
Stwórzmy model potęgowy (model liniowy na zlogarytmowanych zmiennych):
model<-lm(log(mass)~log(size))
summary(model)
##
## Call:
## lm(formula = log(mass) ~ log(size))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.14068 -0.08472 -0.02180 0.10383 0.16000
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -6.6678 0.3307 -20.16 9.66e-07 ***
## log(size) 2.5234 0.0855 29.52 1.00e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1207 on 6 degrees of freedom
## Multiple R-squared: 0.9932, Adjusted R-squared: 0.992
## F-statistic: 871.1 on 1 and 6 DF, p-value: 1.003e-07
Wygląda na to, że nasz model ma postać:
$$\widehat{\text{ln}Y} = -6{,}6678 + {2{,}5234} \text{ln}X,$$czyli inaczej:
$$\widehat{Y} = e^{-6{,}6678} X ^{2{,}5234}$$Sprawdźmy (używając komendy predict), co model przewiduje dla 60-kilogramowego psa:
(prediction<-exp(predict.lm(model, newdata=data.frame(size=c(60)))))
## 1
## 39.00646
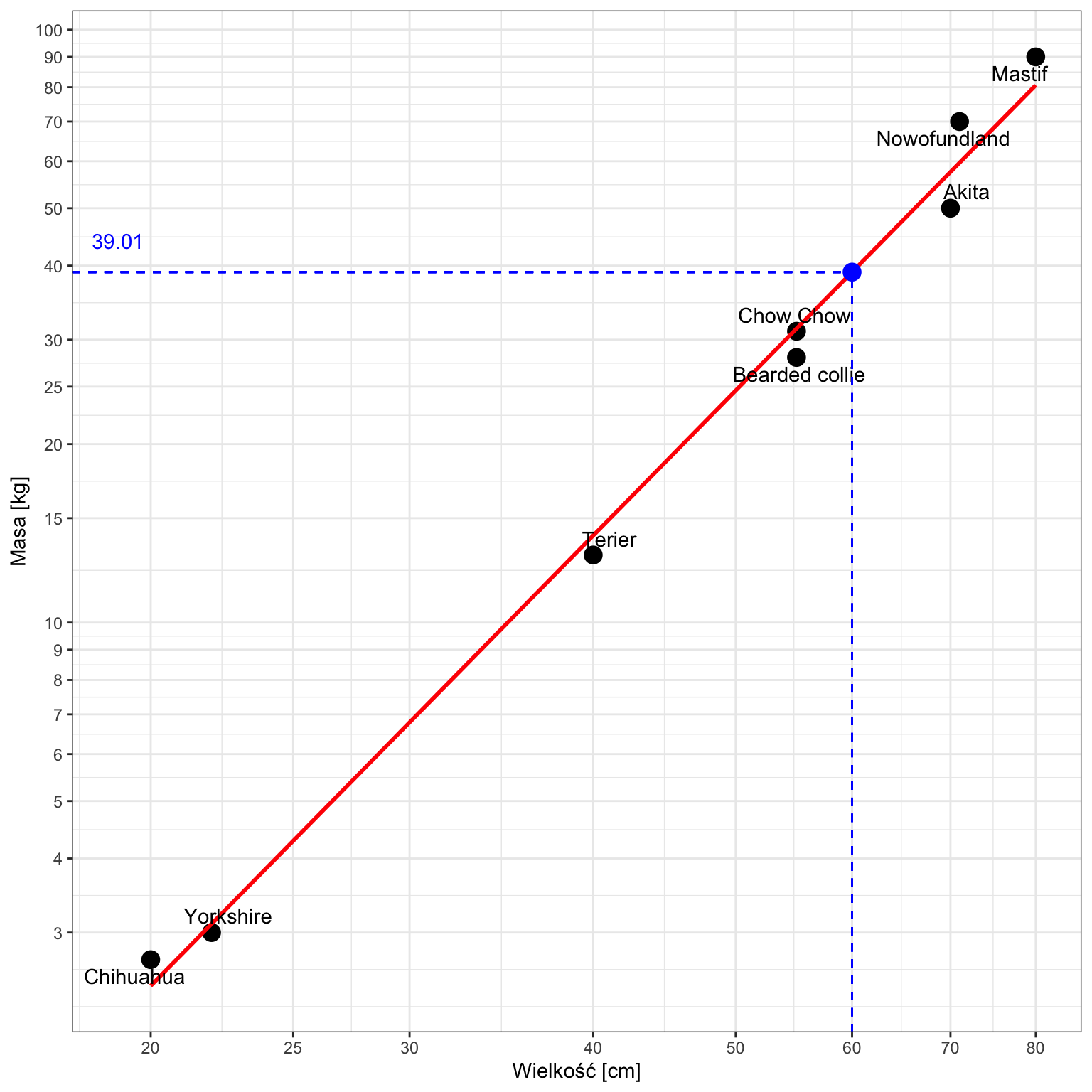
Model przewiduje, że pies będzie ważył około 39,01 kg. Matematycznie wyglądałoby to tak:
$$\widehat{Y} = e^{-6{,}6678} 60 ^{2{,}5234} \approx 39{,}01$$Na wykresie można to przedstawić tak:
ggplot(df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
stat_smooth(method = "lm",
formula = y ~ x,
geom = "smooth",
se=FALSE,
colour='red') +
scale_y_continuous(trans='log10', breaks=yticks) +
scale_x_continuous(trans='log10', breaks=xticks) +
theme_bw() +
geom_point(data=data.frame(size=60, mass=prediction, labels="Nasz Pies"),
aes(x=size, y=mass),
colour='blue',
size=4) +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels))+
geom_segment(aes(x=60, y=0, xend=60, yend=prediction), lty=2, col='blue')+
geom_segment(aes(x=0, y=prediction, xend=60, yend=prediction), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=prediction+5, label=format(round(prediction,2), decimal.mark=',', nsmall=2), col='blue')
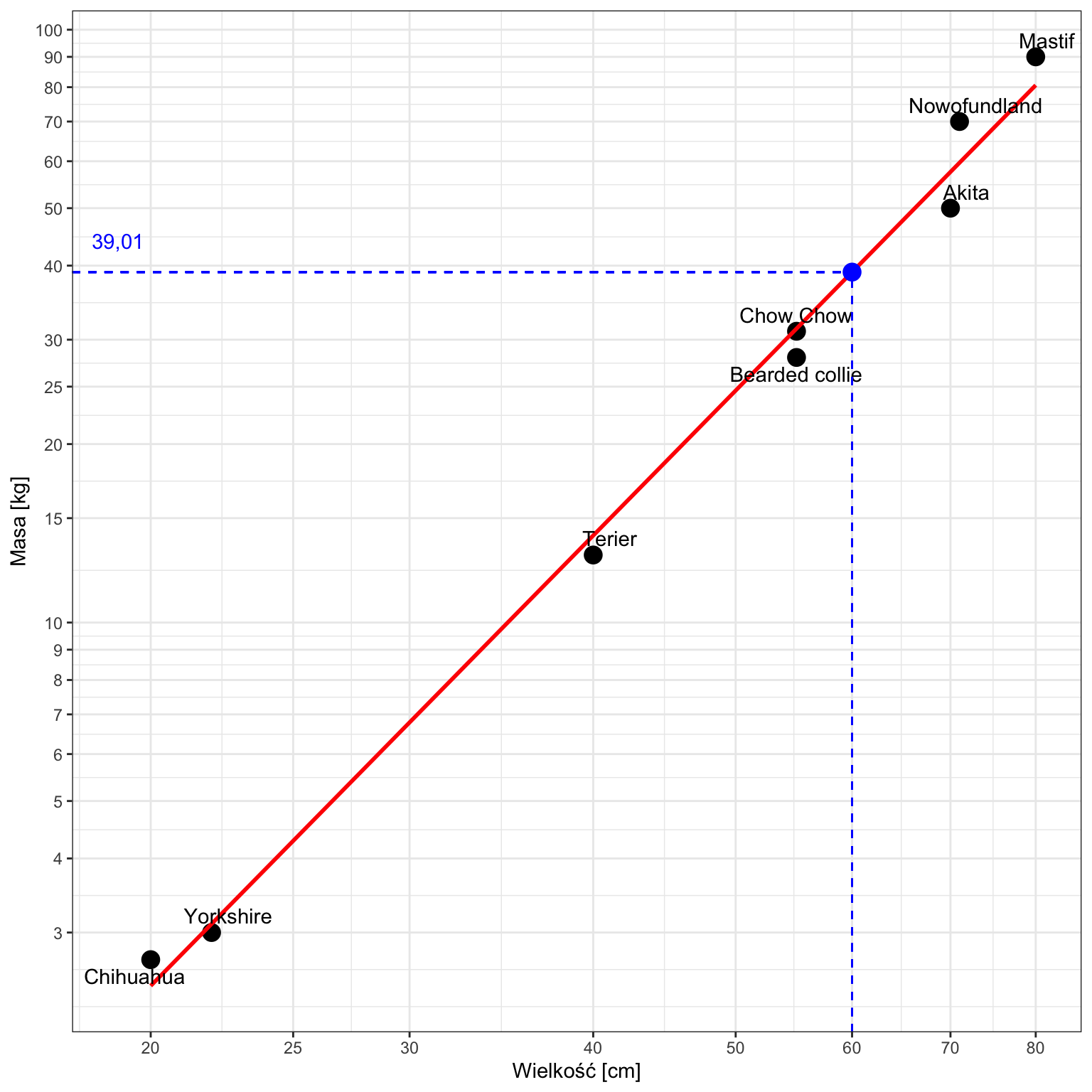
Jeżeli nie chcemy mieć skali logarytmicznej na osiach, wykres będzie wyglądał tak:
ggplot(df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
geom_function(fun=function(x){exp(model$coefficients[1])*x^model$coefficients[2]},
colour='red') +
scale_x_continuous(limits=c(0,90), breaks=sort(c(0:3*25, 60)), expand = c(0, 0)) +
scale_y_continuous(limits=c(0,100), breaks=sort(c(0:4*25, as.numeric(round(prediction,2)))), labels = function(x){format(x,decimal.mark = ",", nsmall=2)}, expand = c(0, 0)) +
theme_bw() +
geom_point(data=data.frame(size=60, mass=prediction, labels="Nasz Pies"),
aes(x=size, y=mass),
colour='blue',
size=4) +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels))+
geom_segment(aes(x=60, y=0, xend=60, yend=prediction), lty=2, col='blue')+
geom_segment(aes(x=0, y=prediction, xend=60, yend=prediction), lty=2, col='blue')
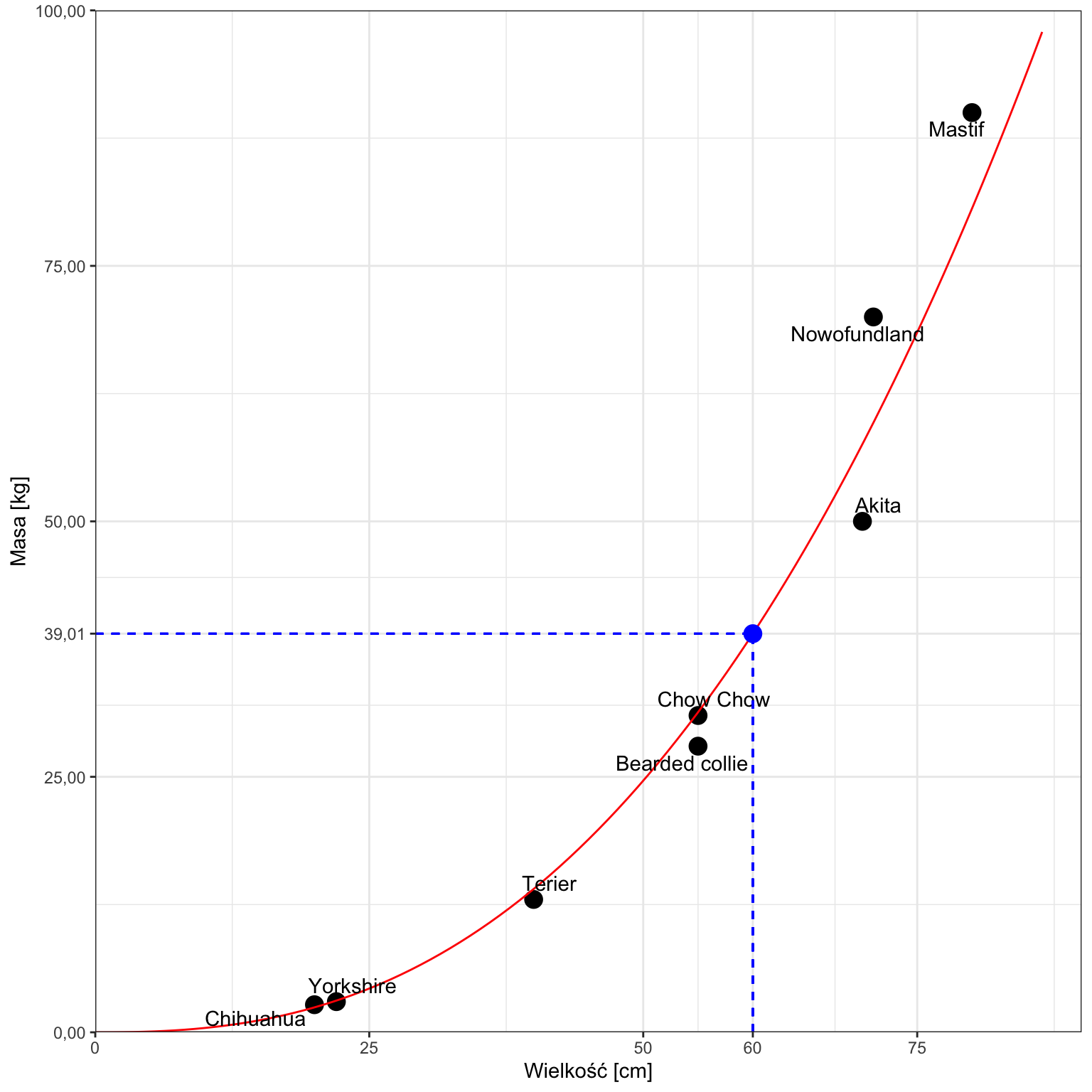
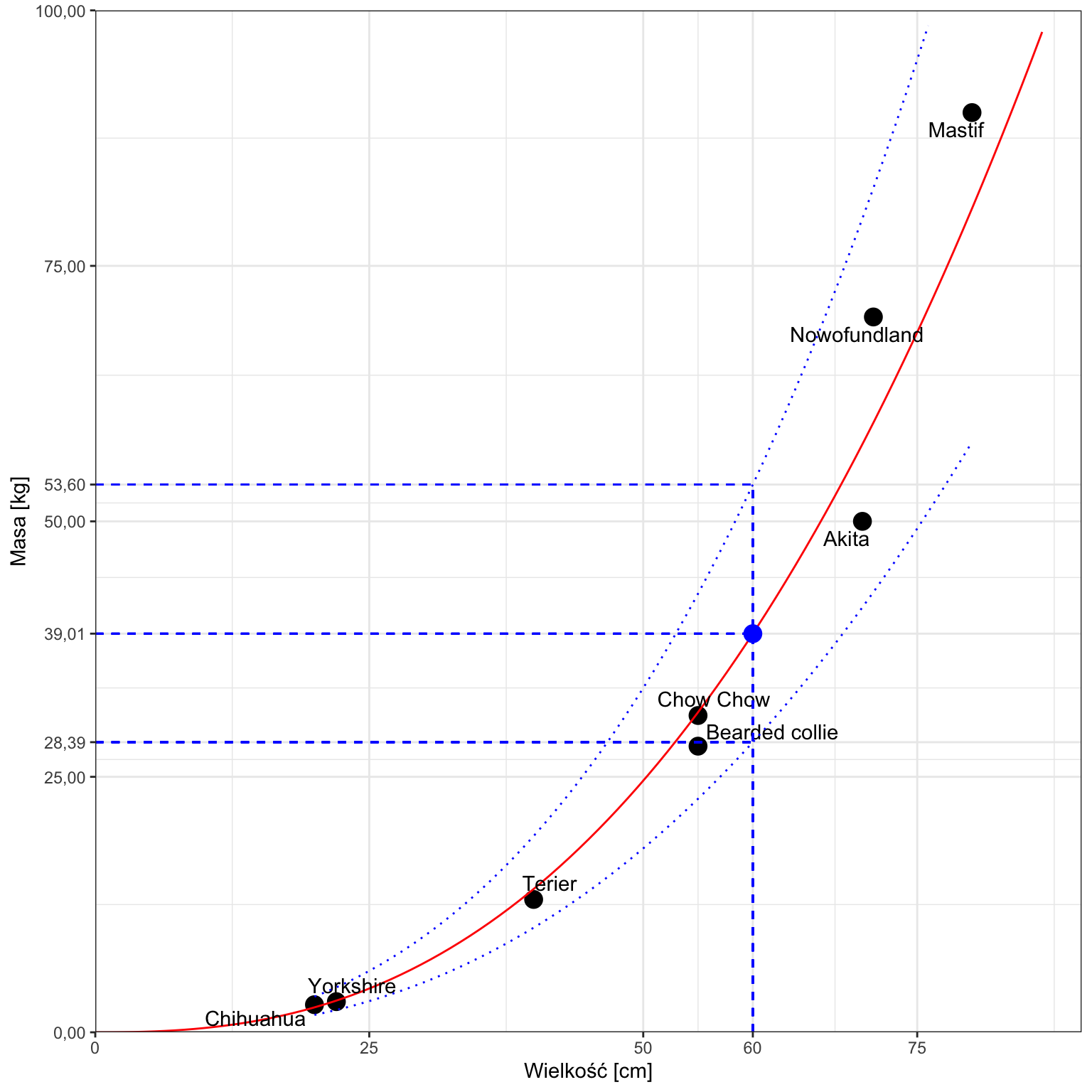
Zamiast oszacowania punktowego możemy zaproponować oszacowanie w formie przedziału. Wymaga to oczywiście przyjęcia, że odpowiednie założenia (wykorzystana próba jest losowa, warunkowy rozkład logarytmu masy jest normalny itd.) przyjnajmniej w przybliżeniu są spełnione.
Przedział predykcji dla 60-centymetrowego psa możemy wyznaczyć w następujący sposób:
(prediction_interval<-exp(predict(
model,
newdata=data.frame(size=c(60)),
interval = "prediction",
level=0.95))
)
## fit lwr upr
## 1 39.00646 28.38695 53.59872
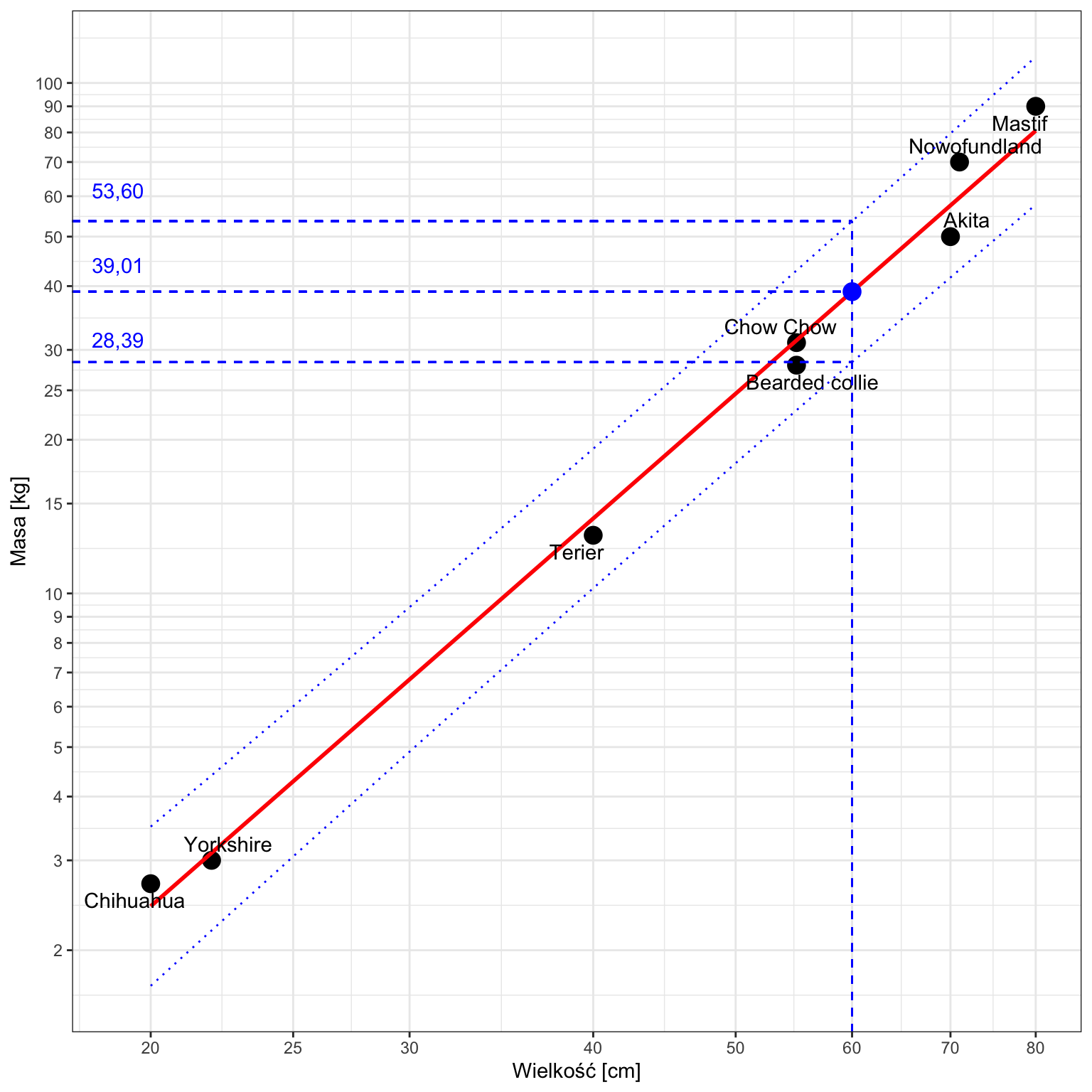
Czyli na poziomie ufności 95% przewidujemy, że 60-centymetrowy pies będzie ważył pomiędzy 28,39 a 53,60 kg.
x4pred<-20:80
df3<-data.frame(exp(predict(model, newdata=data.frame(size=x4pred), interval = "prediction", level=0.95)))
df3$x<-x4pred
ggplot(df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
stat_smooth(method = "lm",
formula = y ~ x,
geom = "smooth",
se=FALSE,
colour='red') +
scale_y_continuous(trans='log10', breaks=yticks) +
scale_x_continuous(trans='log10', breaks=xticks) +
theme_bw() +
geom_point(data=data.frame(size=60, mass=prediction, labels="Nasz Pies"),
aes(x=size, y=mass),
colour='blue',
size=4) +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels)) +
geom_segment(aes(x=60, y=0, xend=60, yend=prediction_interval[,3]), lty=2, col='blue') +
geom_segment(aes(x=0, y=prediction, xend=60, yend=prediction), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=prediction+5, label=format(round(prediction,2), decimal.mark=',', nsmall=2), col='blue') +
geom_line(data=df3, aes(x=x, y=lwr), col='blue', lty=3) +
geom_line(data=df3, aes(x=x, y=upr), col='blue', lty=3) +
geom_segment(aes(x=0, y=lower, xend=60, yend=lower), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=lower+3, label=format(lower, decimal.mark = ',', nsmall=2), col='blue') +
geom_segment(aes(x=0, y=upper, xend=60, yend=upper), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=upper+8, label=format(upper, decimal.mark=',', nsmall=2), col='blue')
ggplot(df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
geom_function(fun=function(x){exp(model$coefficients[1])*x^model$coefficients[2]},
colour='red') +
scale_x_continuous(limits=c(0,90), breaks=sort(c(0:3*25, 60)), expand = c(0, 0)) +
scale_y_continuous(limits=c(0,100), breaks=sort(c(0:4*25, lower, upper, as.numeric(round(prediction,2)))), labels = function(x){format(x,decimal.mark = ",", nsmall=2)}, expand = c(0, 0)) +
theme_bw() +
geom_point(data=data.frame(size=60, mass=prediction, labels="Nasz Pies"),
aes(x=size, y=mass),
colour='blue',
size=4) +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels))+
geom_segment(aes(x=60, y=0, xend=60, yend=upper), lty=2, col='blue')+
geom_segment(aes(x=0, y=prediction, xend=60, yend=prediction), lty=2, col='blue')+
geom_line(data=df3, aes(x=x, y=lwr), col='blue', lty=3) +
geom_line(data=df3, aes(x=x, y=upr), col='blue', lty=3) +
geom_segment(aes(x=0, y=lower, xend=60, yend=lower), lty=2, col='blue') +
geom_segment(aes(x=0, y=upper, xend=60, yend=upper), lty=2, col='blue')
Uzupełnienie 25.05.2024:
W 2024 ważyliśmy Tinę, suczkę pani Dagmary. Tina ma 30 cm.
(prediction_interval<-exp(predict(
model,
newdata=data.frame(size=c(30)),
interval = "prediction",
level=0.95))
)
## fit lwr upr
## 1 6.784646 4.896905 9.400107
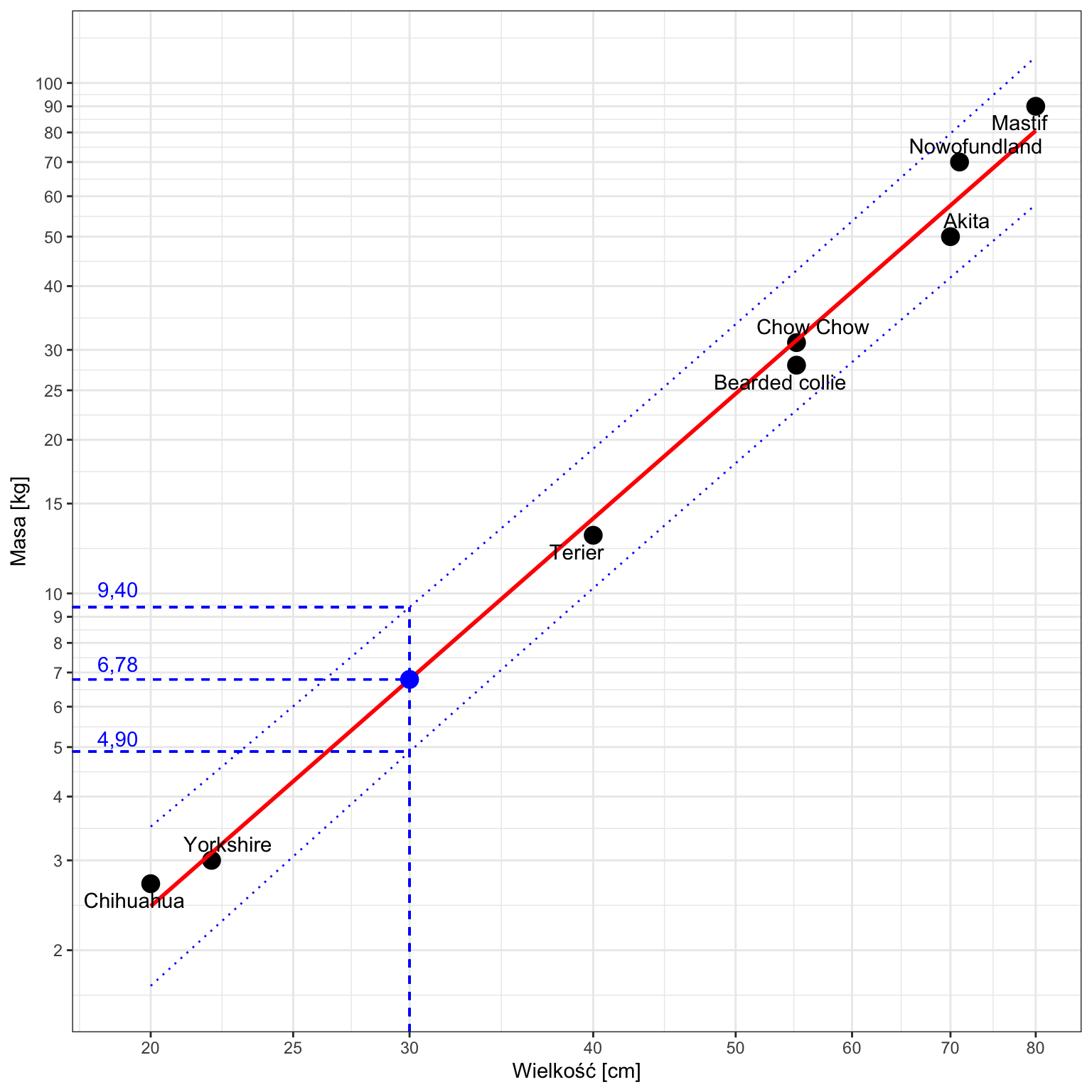
Na poziomie ufności 95% przewidujemy, że 30-centymetrowy pies będzie ważył pomiędzy 4,90 a 9,40 kg.
x4pred<-20:80
prediction<-exp(predict.lm(model, newdata=data.frame(size=c(30))))
ggplot(df, aes(x=size, y=mass)) +
geom_point(size=4) +
xlab("Wielkość [cm]") +
ylab("Masa [kg]") +
stat_smooth(method = "lm",
formula = y ~ x,
geom = "smooth",
se=FALSE,
colour='red') +
scale_y_continuous(trans='log10', breaks=yticks) +
scale_x_continuous(trans='log10', breaks=xticks) +
theme_bw() +
geom_point(data=data.frame(size=30, mass=prediction, labels="Tina"),
aes(x=size, y=mass),
colour='blue',
size=4) +
geom_text_repel(data=df, aes(x=size, y=mass, label=labels)) +
geom_segment(aes(x=30, y=0, xend=30, yend=prediction_interval[,3]), lty=2, col='blue') +
geom_segment(aes(x=0, y=prediction, xend=30, yend=prediction), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=prediction+.5, label=format(round(prediction,2), decimal.mark=',', nsmall=2), col='blue') +
geom_line(data=df3, aes(x=x, y=lwr), col='blue', lty=3) +
geom_line(data=df3, aes(x=x, y=upr), col='blue', lty=3) +
geom_segment(aes(x=0, y=lower, xend=30, yend=lower), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=lower+.3, label=format(lower, decimal.mark = ',', nsmall=2), col='blue') +
geom_segment(aes(x=0, y=upper, xend=30, yend=upper), lty=2, col='blue') +
annotate("text", x=min(xticks)-1, y=upper+.8, label=format(upper, decimal.mark=',', nsmall=2), col='blue')